Шукати в цьому блозі

понеділок, 15 лютого 2016 р.

Обернені тригонометричні функції


Матеріал з Вікіпедії — вільної енциклопедії.
Обернені тригонометричні функції (аркфункції) — математичні функції, що є оберненими до тригонометричних функцій.
До обернених тригонометричних функцій відносять 6 функцій:
  • аркси́нус (arcsin)
  • аркко́синус (arccos)
  • аркта́нгенс (arctg; в іноземній літературі arctan)
  • арккота́нгенс (arcctg; в іноземній літературі arccot чи arccotan)
  • арксе́канс (arcsec)
  • арккосе́канс (arccosec; в іноземній літературі arccsc)
Назва оберненої тригонометричної функції утворюється від назви тригонометриної функції за допомогою префікса «арк-» (від лат. arc — дуга). Це тому, що геометрично значення оберненої тригонометричної функції рівне дузі одиничного кола (чи кутові, що стягує цю дугу), яка опирається на заданий відрізок.

Назва Позначення Визначення Можливі значення для x
(для дійсних чисел)		 Область значень
(радіани)		 Область значень
(градуси)
арксинус y = arcsin x x = sin y −1 ≤ x ≤ 1 −π/2 ≤ y ≤ π/2 −90° ≤ y ≤ 90°
арккосинус y = arccos x x = cos y −1 ≤ x ≤ 1 0 ≤ y ≤ π 0° ≤ y ≤ 180°
арктангенс y = arctg x x = tg y всі дійсні числа −π/2 < y < π/2 −90° < y < 90°
арккотангенс y = arcctg x x = ctg y всі дійсні числа 0 < y < π 0° < y < 180°
арксеканс y = arcsec x x = sec y x ≤ −1 or 1 ≤ x 0 ≤ y < π/2 or π/2 < y ≤ π 0° ≤ y < 90° or 90° < y ≤ 180°
арккосеканс y = arccosec x x = cosec y x ≤ −1 or 1 ≤ x −π/2 ≤ y < 0 or 0 < y ≤ π/2 -90° ≤ y < 0° or 0° < y ≤ 90°

Основні відношення

Головні значення функцій arcsin(x) та arccos(x).
Головні значення функцій arcsec(x) та arccsc(x).
Доповнювальний кут:
\arccos{x} = \frac{\pi}{2} - \arcsin{x}
\arccot{x} = \frac{\pi}{2} - \arctan{x}
\arccsc{x} = \frac{\pi}{2} - \arcsec{x}
від'ємний аргумент:
\arcsin{(-x)} = - \arcsin{x} \!
\arccos{(-x)} = \pi - \arccos{x} \!
\arctan{(-x)} = - \arctan{x} \!
\arccot{(-x)} = \pi - \arccot{x} \!
\arcsec{(-x)} = \pi - \arcsec{x} \!
\arccsc{(-x)} = - \arccsc{x} \!
Обернений аргумент:
\arccos (1/x) \,= \arcsec x \,
\arcsin (1/x) \,= \arccsc x \,
\arctan (1/x) = \tfrac{1}{2}\pi - \arctan x =\arccot x,\text{ if }x > 0 \,
\arctan (1/x) = -\tfrac{1}{2}\pi - \arctan x = -\pi + \arccot x,\text{ if }x < 0 \,
\arccot (1/x) = \tfrac{1}{2}\pi - \arccot x =\arctan x,\text{ if }x > 0 \,
\arccot (1/x) = \tfrac{3}{2}\pi - \arccot x = \pi + \arctan x,\text{ if }x < 0 \,
\arcsec (1/x) = \arccos x \,
\arccsc (1/x) = \arcsin x \,
Якщо наявна тільки частина таблиці для sine:
\arccos x = \arcsin \sqrt{1-x^2},\text{ if }0 \leq x \leq 1
\arctan x = \arcsin \frac{x}{\sqrt{x^2+1}}
Із формули половинного кута \tan \frac{\theta}{2} = \frac{\sin \theta}{1+\cos \theta} , отримаємо:
\arcsin x = 2 \arctan \frac{x}{1+\sqrt{1-x^2}}
\arccos x = 2 \arctan \frac{\sqrt{1-x^2}}{1+x},\text{ if }-1 < x \leq +1
\arctan x = 2 \arctan \frac{x}{1+\sqrt{1+x^2}}

Відношення між оберненими тригонометричними та тригонометричними функціями

\sin (\arccos x) = \cos(\arcsin x) = \sqrt{1-x^2}
\sin (\arctan x) = \frac{x}{\sqrt{1+x^2}}
\cos (\arctan x) = \frac{1}{\sqrt{1+x^2}}
\tan (\arcsin x) = \frac{x}{\sqrt{1-x^2}}
\tan (\arccos x) = \frac{\sqrt{1-x^2}}{x}

Диференціювання тригонометричних функцій

Похідна для дійсних та комплексних значень x: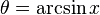
\begin{align} \frac{d}{dx} \arcsin x & {}= \frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx} \arccos x & {}= \frac{-1}{\sqrt{1-x^2}}\\ \frac{d}{dx} \arctan x & {}= \frac{1}{1+x^2}\\ \frac{d}{dx} \arccot x & {}= \frac{-1}{1+x^2}\\ \frac{d}{dx} \arcsec x & {}= \frac{1}{x\,\sqrt{x^2-1}}\\ \frac{d}{dx} \arccsc x & {}= \frac{-1}{x\,\sqrt{x^2-1}} \end{align}
Тільки для дійсних значень x:
\begin{align} \frac{d}{dx} \arcsec x & {}= \frac{1}{|x|\,\sqrt{x^2-1}}; \qquad |x| > 1\\ \frac{d}{dx} \arccsc x & {}= \frac{-1}{|x|\,\sqrt{x^2-1}}; \qquad |x| > 1 \end{align}
Приклад знаходження похідної: нехай \theta = \arcsin x \!, отримаємо:
\frac{d \arcsin x}{dx} = \frac{d \theta}{d \sin \theta} = \frac{1} {\cos \theta} = \frac{1} {\sqrt{1-\sin^2 \theta}} = \frac{1}{\sqrt{1-x^2}}
Опубліковано о
Мітки:

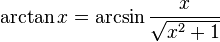
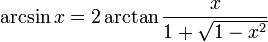
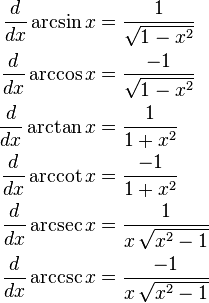
Немає коментарів:

Дописати коментар

Примітка: лише член цього блогу може опублікувати коментар.

Підписатися на: Дописати коментарі (Atom)