Шукати в цьому блозі

понеділок, 15 лютого 2016 р.

Нерівність Коші — Буняковського


Матеріал з Вікіпедії — вільної енциклопедії.
Нерівність Коші—Буняковського (Коші-Шварца; англ. Cauchy–Schwarz inequality, англ. Cauchy–Schwarz–Bunyakovsky inequality) — нерівність, що зв'язує норму та скалярний добуток векторів векторного простору.
Еквівалентно нерівності трикутника для норми в просторі зі скалярним добутком.
Знаходить застосування в лінійній алгебрі для векторів, в математичному аналізі для нескінченних рядів та інтегрування добутків та в теорії ймовірностей при застосуванні до варіації та коваріації.
Нерівність для сум було опубліковано Оґюстеном Коші (1821) (тому цей випадок називають — Нерівність Коші), а відповідна нерівність для інтегралів була вперше сформульована Віктором Буняковським (1859) та вдруге відкрита Германом Шварцем (1888).

Формулювання

Загальний випадок

Для довільних векторів 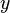\ x, \ y із прегільбертового простору виконується наступна нерівність:
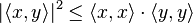|\langle x,y\rangle|^2 \leq \langle x,x\rangle \cdot \langle y,y\rangle,
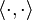де \langle \cdot, \cdot \rangle — операція скалярного добутку, а \ |\cdot|  — модуль числа.
Якщо означити норму, то нерівність можна записати як:
|\langle x,y\rangle| \leq \|x\| \cdot \|y\|.
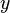Причому рівність виконується лише у випадку коли вектори \ x , \ y лінійно залежні.

Часткові випадки

Лінійний простір \R^n

Скалярний добуток векторів \ x=(x_1,x_2,\ldots x_n) і \ y=(y_1,y_2,\ldots y_n) означимо за формулою
\langle x,y \rangle=\sum\limits_{i=1}^{n} x_iy_i ,
тоді отримаємо, що для дійсних чисел \ x_1,x_2,\ldots x_n,y_1,y_2, \ldots y_n виконується нерівність
\left(\sum_{i=1}^n x_i y_i\right)^2\leq \left(\sum_{i=1}^n x_i^2\right) \left(\sum_{i=1}^n y_i^2\right).
у заданій формі нерівність Коші-Буняковського часто використовується на математичних олімпіадах.

Лінійний простір \ C[a;b]

\ C[a;b] — лінійний простір неперервних на відрізку \ C[a;b] функцій.
Скалярний добуток для функцій \ f(x), g(x)\in C[a;b] означимо через
\langle f(x),g(x) \rangle=\int\limits_{a}^{b} f(x)g(x)\,dx , то виконуватиметься нерівність
\left|\int\limits_{a}^{b} f(x) g(x)\,dx\right|^2\leq\int\limits_{a}^{b} \left|f(x)\right|^2\,dx \cdot \int\limits_{a}^{b}\left|g(x)\right|^2\,dx.

Доведення

Загальний випадок

Для довільного \lambda\in\R. Розглянемо скалярний квадрат вектора \ x+\lambda y:
0 \le \langle x+\lambda y, x+\lambda y \rangle = \langle x, x \rangle + 2\lambda \langle x, y \rangle+\lambda^2 \langle y, y \rangle
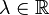Отримуємо квадратичну нерівність \lambda^2\|y\|^2+2\lambda\langle x,y \rangle + \|x\|^2\ge 0 для всіх \lambda \in \R. Це можливо, тоді і тільки тоді, коли її дискримінант 4\langle x,y \rangle^2 - 4\|x\|^2\|y\|^2 не більший від нуля.
Звідки отримуємо \langle x,y \rangle\le\|x\| \cdot \|y\|.

Частковий випадок

Лінійний простір \R^n

В лінійному просторі \R^n з введеним скалярним добутком \langle x,y \rangle=\sum\limits_{i=1}^{n} x_iy_i нерівність Коші-Буняковського можна довести і по іншому, зокрема так
\sum\limits_{i=1}^n \sum\limits_{j=1}^n \left( x_i y_j - x_j y_i \right)^2 = \sum_{i=1}^n x_i^2 \sum_{j=1}^n y_j^2 + \sum_{j=1}^n x_j^2 \sum_{i=1}^n y_i^2 - 2 \sum_{i=1}^n x_i y_i \sum_{j=1}^n x_j y_j
або після зведення однакових доданків
\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \left( x_i y_j - x_j y_i \right)^2 = \sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n x_i y_i \right)^2 .
Оскільки ліва чатина останньої тотожності завжди є невід'ємною, бо є сумою квадратів, то права також приймає невід'ємні значення, звідки негайно слідує нерівність Коші-Буняковського в лінійному просторі \R^n
\sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n x_i y_i \right)^2 \geq 0.

Найвідоміші застосування нерівності Коші-Буняковського

Нерівність трикутника

\begin{align} \|x + y\|^2 & = \langle x + y, x + y \rangle \\ & = \|x\|^2 + \langle x, y \rangle + \langle y, x \rangle + \|y\|^2 \\ & \le \|x\|^2 + 2|\langle x, y \rangle| + \|y\|^2 \\ & \le \|x\|^2 + 2\|x\|\|y\| + \|y\|^2 \\ & = \left(\|x\| + \|y\|\right)^2, \end{align}
добувши корінь з обидвох частин, отримаємо нерівність трикутника.

Математичні олімпіади

На математичних олімпіадах часто використовують наслідок з нерівності Коші-Буняковського для лінійного простору \R^n:
для додатніх дійсних \ a_1, a_2, \ldots a_n, b_1, b_2 \ldots b_n
\dfrac{a_1^2}{b_1}+\dfrac{a_2^2}{b_2}+\ldots+\dfrac{a_n^2}{b_n} \ge\dfrac{(a_1+a_2+\ldots+a_n)^2}{b_1+b_2+\ldots+b_n}.
Нерівність негайно слідує з нерівності Коші-Буняковського, якщо покласти x_i=\sqrt{\dfrac{a_i^2}{b_i}}, \quad y_i=\sqrt{b_i} .
Зокрема дану нерівність можна використати для доведення нерівності Несбіта:
з нерівностей Коші-Буняковського і трьох квадратів отримуємо:
\dfrac{a^2}{a(b+c)}+\dfrac{b^2}{b(a+c)}+\dfrac{c^2}{c(a+b)}\ge\dfrac{(a+b+c)^2}{2(ab+bc+ac)}\ge\dfrac{3}{2},
з чого негайно слідує нерівність Несбіта.
Опубліковано о
Мітки:

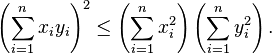
Немає коментарів:

Дописати коментар

Примітка: лише член цього блогу може опублікувати коментар.

Підписатися на: Дописати коментарі (Atom)