Матеріал з Вікіпедії — вільної енциклопедії.
Операції з часом на цих годинниках використовують правила арифметики по модулю 12. 9+4 ≡ 1 mod 12.
Найбільш відомий приклад модульної арифметики, це запис часу в 12-годинному форматі, в якому день ділиться на два 12-годинних періоди. Якщо зараз 9:00, то через 4 години на годиннику буде 1:00. Якщо просто додати, то 9 + 4 = 13, але це не правильна відповідь, тому що на годиннику по досягненні стрілки 12-ї години, замість 12:00 ми отримуємо 00:00. Тому правильна відповідь, що на годиннику буде 1:00.
Аналогічним чином, якщо годинник починає відлік о 12:00 (опівдні) і пройде 21 година, то час буде 9:00 наступного дня, а не 33:00. Оскільки годинник починає новий відлік часу після досягнення 12, то це буде арифметика по модулю 12. 12 відповідає не тільки значенню 12, але також і 0, так що час, який називається «12:00», також може бути названий «0:00», так як 0 ≡ 12 mod 12.
Ще один підхід до модульної арифметики пов'язаний з залишками від ділення цілих чисел на певне задане натуральне число. Фактично в ній розглядаються класи еквівалентності певного натурального числа.
В сучасному вигляді модульна арифметика була розвинута Гаусом в Disquisitiones Arithmeticae[en] (1801).
Зміст
Рівність за модулем
Два цілих числа a і b називаються рівними (конгруентними) за модулем n, якщо при цілочисельному діленні на n вони мають однакові залишки. Рівність чисел a і b за модулем n записують так:- Різниця a-b ділиться на n націло. Тобто a - b = kn, де k — якесь ціле число.
- Число a може бути записано у вигляді a = b + kn, де k — якесь ціле число.
Властивості, що виконуються для відношення рівності, виконуються також для рівності за модулем.
Якщо
 і
і  , тоді:
, тоді:Рівність за модулем, як відношення еквівалентності
З визначення рівності за модулем витікають такі властивості:- рефлексивність

- симетричність

- транзитивність: якщо
 та
та  то також
то також 
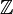 . Тоді
. Тоді 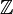 розбивається на класи еквівалентності.
розбивається на класи еквівалентності.Клас еквівалентності відношення рівності за модулем n до якого належить число a позначається
 . Так як,
. Так як,  , то додати n, теж саме, що і додати 0. Тому клас числа
, то додати n, теж саме, що і додати 0. Тому клас числа 
Для прикладу, розглянемо відношення по модулю 2.
 , тоді і тільки тоді, коли їх різниця
, тоді і тільки тоді, коли їх різниця  парне число. Це співвідношення призводить до двох класів
еквівалентності: один клас, що складається з усіх парних чисел, та
другий, який складається з усіх непарних чисел. Клас парних чисел
позначається, як [0], непарних як [1]. Згідно з цим співвідношенням [7], [9], та [117] належать одному класу -
парне число. Це співвідношення призводить до двох класів
еквівалентності: один клас, що складається з усіх парних чисел, та
другий, який складається з усіх непарних чисел. Клас парних чисел
позначається, як [0], непарних як [1]. Згідно з цим співвідношенням [7], [9], та [117] належать одному класу -  .
.Множина класів конгруентності за модулем
 позначається:
позначається:  (або,
(або,  чи
чи  ) і за визначенням це:
) і за визначенням це: має n елементів, і може бути записано:
має n елементів, і може бути записано:Кільце класів рівності за модулем
Таким чином є комутативним кільцем. Наприклад в
є комутативним кільцем. Наприклад в  , маємо
, маємо має обернений елемент тоді і лише тоді коли m i n є взаємно простими числами. Справді, якщо m i n є взаємно простими, то тоді існують
має обернений елемент тоді і лише тоді коли m i n є взаємно простими числами. Справді, якщо m i n є взаємно простими, то тоді існують  такі, що
такі, що  Звідси:
Звідси: і як наслідок
і як наслідок 
 для деякого
для деякого  , то
, то  для деякого
для деякого  , що неможливо, враховуючи взаємну простоту m i n. Відповідно, якщо
, що неможливо, враховуючи взаємну простоту m i n. Відповідно, якщо  просте число, то
просте число, то  є полем.
є полем.Розв'язання лінійних рівнянь
| Вікіпідручник має книгу на тему |
 або за допомогою формули
або за допомогою формули якщо НСД
якщо НСД  тобто взаємно прості числа.
тобто взаємно прості числа.
 — функція Ейлера, яка дорівнює кількості натуральних чисел, не більших n і взаємно простих з ним.
— функція Ейлера, яка дорівнює кількості натуральних чисел, не більших n і взаємно простих з ним.Якщо НСД
 , порівняння або має не єдине рішення, або не має рішення. Як легко побачити, порівняння
, порівняння або має не єдине рішення, або не має рішення. Як легко побачити, порівнянняІнше порівняння






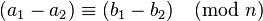
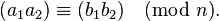










Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.