Матеріал з Вікіпедії — вільної енциклопедії.
Алгебра логіки (Булева логіка, двійкова логіка, двійкова алгебра) — розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями.[1] Найчастіше передбачається, що висловлювання можуть бути тільки істинними або помилковими, тобто використовується так звана бінарна або двійкова логіка, на відміну від, наприклад, тризначної логіки.
| Алгебра логіки як алгебраїчна структура наряду з алгеброю множин є частковими випадками булевої алгебри. |
Визначення
Базовими елементами, якими оперує алгебра логіки, є висловлювання.Висловлювання будуються над множиною {B,
 ,
,  ,
,  , 0, 1}, де B — непорожня множина, над елементами якої визначені три операції:
, 0, 1}, де B — непорожня множина, над елементами якої визначені три операції: заперечення (унарна операція),
заперечення (унарна операція), кон'юнкція (бінарна),
кон'юнкція (бінарна), диз'юнкція (бінарна),
диз'юнкція (бінарна),- а логічний нуль 0 і логічна одиниця 1 — константи.
- диз'юнкт — пропозиціональна формула, що є диз'юнкцією одного або більше літералів (наприклад
 ).
). - кон'юнктив — пропозиціональна формула, що є кон'юнкцією одного або більше літералів (наприклад
 ).
).
 ) або у вигляді риси над операндом (
) або у вигляді риси над операндом ( ), що компактніше, але в цілому менш помітно.
), що компактніше, але в цілому менш помітно.Аксіоми
Походження
Засади алгебри логіки було сформульовано британцем Джорджем Булем в 1847 році. Пізніше її розвивали Чарлз Пірс, Генрі Шеффер, П. С. Порецький, Бертран Рассел, Давид Гільберт та ін.Відтоді ця система застосовується для вирішення широкого спектру проблем математичної логіки та теорії множин, та особливо конструювання цифрової електроніки (початок використання алгебри логіки для синтезу перемикальних (релейних) схем був покладений в 1938 році роботами відомого американського вченого Клода Шеннона).
Предмет вивчення
Спочатку проблематика алгебри логіки перетиналась з проблематикою алгебри множин (теоретико-множинні операції).Проте із закінченням формування теорії множин (70-і роки 19 ст.), яка включила в себе алгебру множин, і подальшим розвитком математичної логіки, предмет алгебри логіки значно змінився.
Сучасна алгебра логіки розглядає операції над висловлюваннями (див. Числення висловлень), як булеву функцію і вивчає відносно них такі питання, як:
- таблиці істинності;
- функціональна повнота;
- замкнені класи;
- представлення у вигляді: ДНФ, КНФ, полінома Жегалкіна.
Логічні операції
Простим і найширше вживаним прикладом такої алгебраїчної системи є множина B, що складається всього з двох елементів :- B = { Хибність (0), Істина (1) }
Спираючись на цей математичний інструментарій, логіка висловлювань вивчає висловлювання і предикати. Також вводяться додаткові операції, такі як еквівалентність
 («тоді і тільки тоді, коли»), імплікація
(«тоді і тільки тоді, коли»), імплікація  («отже»), складання по модулю два
(«отже»), складання по модулю два  («виключна диз'юнкція»), штрих Шефера
(«виключна диз'юнкція»), штрих Шефера  , стрілка Пірса
, стрілка Пірса  та інші.
та інші.Логіка висловлювань послужила основним математичним інструментом при створенні комп'ютерів. Вона легко перетворюється в бітову логіку: істинність висловлювання позначається одним бітом (0 — ХИБНІСТЬ, 1 — ІСТИНА); тоді операція
 набуває суті вирахування з одиниці;
набуває суті вирахування з одиниці;  — немодульного додавання; & — множення;
— немодульного додавання; & — множення;  — рівності;
— рівності;  — в буквальному розумінні сума за модулем 2 (виключне АБО — XOR);
— в буквальному розумінні сума за модулем 2 (виключне АБО — XOR);  — сума не перевищує 1 (тобто A
— сума не перевищує 1 (тобто A  B = (A + B) <= 1).
B = (A + B) <= 1).Згодом булеву алгебру було узагальнено від логіки висловлювань шляхом введення характерних для логіки висловлювань аксіом. Це дозволило розглядати, наприклад, логіку кубітів, потрійну логіку (коли є три варіанти істинності висловлювання: «істина», «хибність» і «невизначено») тощо.
Властивості логічних операцій
- Комутативність: x
 y = y
y = y x,
x,  {&,
{&, 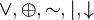 }.
}. - Ідемпотентність: x
 x = x,
x = x,  {&,
{&,  }.
}. - Асоціативність: (x
 y)
y) z = x
z = x (y
(y z),
z),  {&,
{&,  }.
}. - Дистрибутивність кон'юнкцій і диз'юнкції відносно диз'юнкції, кон'юнкції і суми за модулем два відповідно:
 ,
,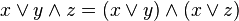 ,
, .
.
- Закони де Мо́ргана:
 ,
, .
.
- Закони поглинання :
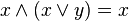 ,
, .
.
- Інші (1):
- Інші(2) :
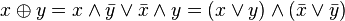 .
.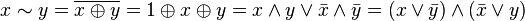 .
. .
. .
.
- Інші(3) (Доповнення законів де Мо́ргана) :
 .
. .
.
 ,
, 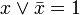

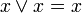
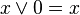

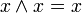
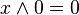
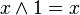
 .
. .
. .
.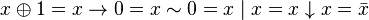 .
.
Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.