Шукати в цьому блозі

вівторок, 16 лютого 2016 р.

Описане коло


Матеріал з Вікіпедії — вільної енциклопедії.
Circumscribed Polygon.svg
Описане коло многокутника — коло, що містить всі вершини многокутника. Центром є точка (прийнято позначати O) перетину серединних перпендикулярів до сторін многокутника.
Центр описаного кола опуклого n-кутника лежить на точці перетину серединних перпендикулярів його сторін. Звідси випливає, що коли навколо n-кутника побудоване описане коло, то всі серединні перпендикуляри до його сторін перетинаються в одній точці (центрі кола).
Навколо будь-якого правильного многокутника можна описати коло.

Трикутник

Коло, описане довкола трикутника
  • У гострокутного трикутника центр описаного кола лежить всередині, у тупокутного - поза трикутником, у прямокутного - на середині гіпотенузи.
  • Гострокутний
  • Тупокутний
  • Прямокутний
Позначаємо літерою О точку перетину серединних перпендикулярів до його сторін та проведемо відрізки ОА, ОВ і ОС. Оскільки точка О рівновіддалена від вершин трикутника АВС, то ОА = OB = ОС. Тому коло з центром О радіусу ОА проходить через всі три вершини трикутника і, отже, є описаним навколо трикутника ABC.
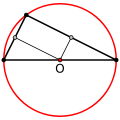
  • 3 з 4 кіл, описаних відносно серединних трикутників (утворених середніми лініями трикутника), перетинаються в одній точці всередині трикутника. Ця точка і є центром описаного кола основного трикутника.
  • Центр описаного навколо трикутника кола служить ортоцентром трикутника з вершинами на серединах сторін даного трикутника. Ортоцентр трикутника - це точка перетину висот трикутника або їх продовжень.
  • Відстань від вершини трикутника до ортоцентру вдвічі більше, ніж відстань від центру описаного кола до протилежної сторони.
  • Радіус описаного кола можна знайти за формулами:
R = \frac {abc}{4S}
R = \frac {a}{2\sin\alpha}
R = \frac{abc}{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}} = \frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}}
Де:
a, b, c — сторони трикутника,
\alpha — кут, що лежить навпроти сторони a,
p — півпериметр трикутника.
S — площа трикутника.
  • Положення центру описаного кола.
Нехай ~ {\mathbf r}_A, {\mathbf r}_B, {\mathbf r}_C радіус-вектори вершин трикутника, ~ \mathbf{r}_O — радіус-вектор центру описаного кола. Тоді
~ \mathbf{r}_O= \alpha_A\mathbf{r}_A + \alpha_B\mathbf{r}_B+\alpha_C\mathbf{r}_C
де
\alpha_A = \frac{a^2}{8S^2}(\mathbf{r}_A-\mathbf{r}_B,\mathbf{r}_A-\mathbf{r}_C), \qquad \alpha_B = \frac{b^2}{8S^2}(\mathbf{r}_B-\mathbf{r}_A,\mathbf{r}_B-\mathbf{r}_C), \qquad \alpha_C = \frac{c^2}{8S^2}(\mathbf{r}_C-\mathbf{r}_A,\mathbf{r}_C-\mathbf{r}_B)
  • Рівняння описаного кола.
Нехай~ {\mathbf r}_A = (x_A, y_A), {\mathbf r}_B = (x_B, y_B), {\mathbf r}_C= (x_C, y_C) координати вершин трикутника в певній декартовій системі координат на площині, ~ \mathbf{r}_O= (x_O, y_O) — координати центру описаного кола. Тоді
x_O=\frac{1}{4S}\begin{vmatrix} x_A^2 + y_A^2 & y_A & 1 \\ x_B^2 + y_B^2 & y_B & 1 \\ x_C^2 + y_C^2 & y_C & 1 \end{vmatrix} \qquad y_O=-\frac{1}{4S}\begin{vmatrix} x_A^2 + y_A^2 & x_A & 1 \\ x_B^2 + y_B^2 & x_B & 1 \\ x_C^2 + y_C^2 & x_C & 1 \end{vmatrix}
а рівняння описаного кола має вигляд
\begin{vmatrix} x^2 + y^2 & x & y & 1 \\ x_A^2 + y_A^2 & x_A & y_A & 1 \\ x_B^2 + y_B^2 & x_B & y_B & 1 \\ x_C^2 + y_C^2 & x_C & y_C & 1 \end{vmatrix} =0
Для точок ~(x, y), що лежать всередині кола, визначник негативний, а для точок поза нею - позитивний.

  • Теорема про тризубець : Якщо W - точка перетину бісектриси кута A з описаним колом, а I - центр вписаного кола то |WI|=|WB|=|WC|.
  • Формула Ейлера : Якщо d - відстань між центрами вписаного і описаного кіл, а їхні радіуси дорівнюють r і R відповідно, то d^2 = R^2 - 2Rr.

Чотирикутник

Cyclic quadrilateral.svg
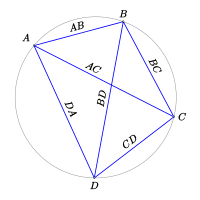
Малюнок до теореми Птолемея
Вписаний простий (без самоперетинів) чотирикутник обов'язково є опуклим .
Навколо опуклого чотирикутника можна описати коло тоді й тільки тоді, коли сума його внутрішніх протилежних кутів дорівнює 180 ° (π радіан).
Радіус описаного кола правильного n-кутника з довжиною сторін a дорівнює:
R = \frac{a}{2 \sin\frac{180^\circ}{n}}
Можна описати коло навколо:
|AC|·|BD| = |AB|·|CD| + |BC|·|AD|

Многокутник

Якщо з відрізків скласти многокутник, то його площа буде максимальною, коли він вписаний.
Опубліковано о
Мітки:

Немає коментарів:

Дописати коментар

Примітка: лише член цього блогу може опублікувати коментар.

Підписатися на: Дописати коментарі (Atom)