Матеріал з Вікіпедії — вільної енциклопедії.
Трикутник
Основні відомості про трикутники були наведені Евклідом в його праці «Елементи» біля 300 до н. е.
Типи трикутників
Ейлерова діаграма видів трикутників.
- В рівносторонньому трикутнику всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють 60°. Рівносторонній трикутник ще називають правильним.
- В рівнобедреному трикутнику дві сторони мають однакову довжину, третя сторона при цьому називається основою трикутника. Рівнобедрений трикутник має два однакові кути, які знаходяться при його основі.
- Різносторонній трикутник має сторони різної довжини. Внутрішні кути різностороннього трикутника різні.
- Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника.
- Тупокутний трикутник має один внутрішній кут більший ніж 90°.
- В гострокутному трикутнику всі кути менші за 90°. Рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.
Точки й лінії пов'язані з трикутником
Є сотні різноманітних побудов для визначення особливих точок всередині трикутника, які задовольняють деякі унікальні умови (дивись в списку посилань перелік статей). Часто необхідно побудувати три прямі, що пов'язані аналогічно із трьома сторонами (вершинами, кутами) трикутника і тоді переконатись, що вони перетинаються в одній точці. Важливим інструментом для перевірки цього є теорема Чеви, яка дає критерії для визначення конкурентності прямих. Подібно до цього, лінії пов'язані з трикутником часто будуються після перевірки, що три аналогічним чином отримані точки є колінеарні — теорема Менелая дає для цього випадку загальний критерій. В цьому розділі приведені тільки такі побудови, що найбільш часто зустрічаються.Серединний перпендикуляр трикутника — це перпендикуляр, який проходить посередині сторони трикутника. Три серединні перпендикуляри перетинаються в одній точці, яка є центром описаного кола. Діаметр описаного кола можна визначити з теореми синусів.
Виходячи з теореми Фалеса, можна стверджувати, якщо центр описаного кола розміщений на одній із сторін трикутника, тоді протилежний кут прямий. Більше того, якщо центр описаного кола знаходиться всередині трикутника, то трикутник гострокутний, а якщо назовні, то трикутник тупокутний.

Три висоти трикутника перетинаються в ортоцентрі.

На перетині трьох бісектрис трикутника знаходиться центр вписаного кола.

Барицентр — центр мас трикутника.
Середні точки трьох сторін і основи трьох висот всі лежать на одному колі, яке називається колом дев'яти точок трикутника. Решта три точки, через які коло отримало свою назву, це середини тієї частини висоти, що лежить між ортоцентром і вершиною. Радіус кола дев'яти точок дорівнює половині описаного кола. Воно дотикається до вписаного кола (в точці Феєрбаха) та до трьох зовнівписаних кіл.
Лінія Ейлера.
Основні факти
Позначення
Сума внутрішніх кутів трикутника — 180 градусів. Зовнішній кут трикутника (кут суміжний до внутрішнього кута) завжди дорівнює сумі двох інших внутрішніх кутів трикутника. Як і у всіх випуклих багатогранників сума зовнішніх кутів трикутника 360 градусів.
Два трикутники називаються подібними тоді і тільки тоді, якщо кути одного рівні відповідним кутам іншого. В такому випадку довжини відповідних сторін пропорційні. Так може бути наприклад, коли у двох трикутників є спільний кут, а сторони протилежні цьому куту — паралельні. Ось кілька постулатів і теорем про подібні трикутники:
- Два трикутники подібні, якщо в них хоча б два відповідних кута рівні.
- Якщо дві відповідні сторони в трикутниках пропорційні, а кут між ними однаковий, то трикутники подібні.
- Якщо всі сторони двох трикутників пропорційні, то трикутники подібні.
- Постулат SAS (side-angle-side): Якщо дві сторони і кут між ними в трикутників відповідно рівні, то трикутники конгруентні.
- Постулат SSS: Якщо всі відповідні сторони в трикутників рівні, то трикутники конгруентні.
- Постулат ASA: Якщо сторона і прилеглі до неї кути в трикутників відповідно рівні, то трикутники конгруентні.
- Постулат AAS: Якщо два кути і будь-яка сторона в трикутників відповідно рівні, то трикутники конгруентні.
- Теорема Гіпотенуза-катет: Якщо гіпотенуза і один катет в прямокутних трикутників відповідно рівні, то трикутники конгруентні.
Обчислення площі трикутника
Площа трикутника може бути показана як половина площі паралелограма, який має таку саму основу та висоту.
З використанням векторів
Площу паралелограма можна обчислити за допомогою векторів. Нехай вектори AB і AC спрямовані відповідно від A до B і від A до C. Тоді площа паралелограма ABDC дорівнює |AB × AC|, тобто числове значення векторного добутку AB і AC. |AB × AC| дорівнює |h × AC|, де h — висота паралелограма як вектор.Площа трикутника ABC дорівнює половині площі паралелограма S = ½|AB × AC|.
Площу трикутника ABC також можна обчислити як скалярний добуток векторів.
Тригонометричний спосіб
Висоту трикутника можна визначити використовуючи тригонометричні формули. Згідно з позначенням, як на малюнку зліва, висота дорівнює h = a sin γ. Підставивши висоту в формулу S = ½bh, яка наведена вище, отримаємо:Знаючи сторону і два прилеглі кути:[1]
Використання координат
Якщо точка А розташована в точці відліку (0, 0) Декартової координатної системи, а координати інших двох точок B = (xB, yB) і C = (xC, yC), тоді площа S може бути обчислена як ½ абсолютного значення детермінанту:Формула Герона
Форма трикутника однозначно визначається трьома сторонами. Відповідно для того, щоб порахувати площу, достатньо знати довжину сторін. За формулою Герона: — півпериметр
— півпериметрІнші способи запису формули Герона:
Формули, схожі на формулу Герона
Є три формули, що мають схожі на формулу Герона, але записані через інші величини. Позначивши медіани для сторін a, b, і c відповідно як і
і  , а їхню півсуму
, а їхню півсуму  як
як  , маємо[2]
, маємо[2] ,
,  , і
, і 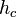 , і познавши півсуму величин, обернених до висот, як
, і познавши півсуму величин, обернених до висот, як  , матимемо[3]
, матимемо[3]![P=[(\sin \ \ \alpha)+(\sin \ \ \beta)+(\sin \ \ \gamma)]/2](https://upload.wikimedia.org/math/e/5/f/e5fc2e81cb269de842d2cd77873d8434.png) , матимемо[4]
, матимемо[4]
Використовуючи Теорему Піка
Див. Теорему Піка для пояснень, як знайти площу довільного цілочислового многокутника.Теорема стверджує, що
Інші формули обчислення площі
Існують також інші формули для обчислення площі, наприклад, 90°.
90°.В 1885 році, Бейкер[6] дав підбірку з більш ніж сотні різних формул для обчислення площі трикутника (хоча варто попередити читача, що деякі з них неправильні). Наводимо тут #9, #39a, #39b, #42, і #49:
Обчислення площі прямокутного трикутника
У прямокутному трикутнику можна взяти один із катетів як основу, а інший — як його висоту. Звідси формула прямокутного трикутника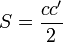
де S — площа, а c і c' — катети.
Обчислення сторін та кутів
Загалом, є різноманітні прийняті методи обчислення довжин сторін та кутів трикутника. Якщо певні методи можуть бути використані тільки в прямокутному трикутнику, то інші можуть виявитись потрібними для складніших випадків.Тригонометричні відношення в прямокутних трикутниках
Прямокутний трикутник
завжди має кут 90° (π/2 радіан), тут позначений C. Кути A і B можуть
бути різними. Тригонометричні функції показують співвідношення між
довжинами сторін і внутрішніми кутами в прямокутному трикутнику.
- Гіпотенуза — сторона протилежна до прямого кута, або найдовша сторона в прямокутному трикутнику, в даному випадку h.
- Протилежний катет — сторона протилежна до кута, що розглядається.
- Прилеглий катет — та сторона, що прилягає до кута, що розглядається і до прямого. В даному випадку прилеглий катет b.
Синус, косинус і тангенс
Синус кута — це відношення довжини протилежного катета до довжини гіпотенузи. В нашому випадкуКосинус кута — це відношення довжини прилеглого катета до довжини гіпотенузи. В нашому випадку
Обернені функції
Обернені тригонометричні функції використовують, щоб обчислити внутрішні кути прямокутного трикутника, якщо відомі довжини будь-яких двох сторін.Arcsin використовують, щоб обчислити кут, якщо відомі довжина протилежної сторони і довжина гіпотенузи
Теореми синусів, косинусів та тангенсів
Трикутник з сторонами довжиною a, b і c та кутами α, β і γ відповідно .
 ,
,  і
і  подібний до трикутника довжина сторін якого дорівнює
подібний до трикутника довжина сторін якого дорівнює  ,
, 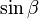 і
і  .
Цей трикутник може бути побудований, якщо накреслити коло діаметром 1 і
вписати в нього два кути вказаного трикутника. Довжина сторін
трикутника буде
.
Цей трикутник може бути побудований, якщо накреслити коло діаметром 1 і
вписати в нього два кути вказаного трикутника. Довжина сторін
трикутника буде  ,
, 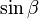 і
і  . Сторона чия довжина
. Сторона чия довжина  протилежна до кута чия величина
протилежна до кута чия величина  , і т. д.
, і т. д.Теорема косинусів, чи правило косинусів, поєднує довжину невідомої сторони трикутника з довжиною інших сторін і з кутом протилежним до невідомої сторони. Згідно з теоремою:
Для трикутника з довжинами сторін
 ,
,  ,
,  і кутами
і кутами  ,
,  ,
,  відповідно, для двох відомих довжин трикутника
відповідно, для двох відомих довжин трикутника  і
і  , і кута між двома відомими сторонами
, і кута між двома відомими сторонами  (чи кута протилежного до невідомої сторони
(чи кута протилежного до невідомої сторони  ), щоб розрахувати довжину третьої сторони можна використати наступну формулу:
), щоб розрахувати довжину третьої сторони можна використати наступну формулу:Ще формули для трикутників Евклідової геометрії
Для всіх трикутників Евклідової геометрії також справедливі такі формули: ,
,
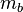 і
і  , з відповідними медіанами і сторонами;
, з відповідними медіанами і сторонами; ,
,
 .
.
Неплощинні трикутники
Трикутник на сфері.
Якщо сума внутрішніх кутів трикутника в площині завжди дорівнює 180°, то для гіперболічного трикутника сума кутів буде меншою 180°, а для сферичного трикутника сума кутів буде більшою 180°. Гіперболічний трикутник можна отримати на негативно вигнутій поверхні, наприклад гіперболічний параболоїд, а сферичний трикутник можна отримати на позитивно вигнутій поверхні, наприклад сфера. Таким чином, якщо зобразити гігантський трикутник на поверхні Землі, то отримаєм суму кутів більшу ніж 180°; фактично сума буде лежати в проміжку 180° і 540°[9] Зокрема можна зобразити трикутник на сфері таким чином, що кожен внутрішній кут буде дорівнювати 90°, а сума всіх кутів 270°.
Зокрема, на сфері сума кутів трикутника дорівнює
- 180°×(1+4f),
З формули вище ми також бачимо, що в певному наближенні поверхню землі можна вважати плоскою: якщо зобразити довільний малий трикутник на поверхні Землі, тоді частка f земної поверхні, яка обмежена даним трикутником буде близька до нуля. Наприклад, відомо що площа земної поверхні 510 млн км², тоді для трикутника площею 10 000 км², отримаєм суму кутів 180.01°.





















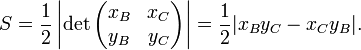
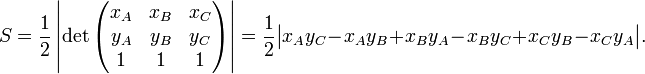





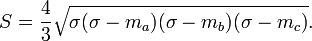
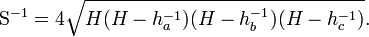
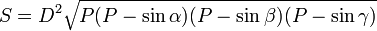




![S = \frac{1}{2}[abch_ah_bh_c]^{1/3},](https://upload.wikimedia.org/math/5/d/2/5d2a4e4fd88ef1b1dc072b0d59a30920.png)



















![\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}.](https://upload.wikimedia.org/math/c/3/4/c34b871436dbf7e3a62c5337536ab791.png)

![\text{Довжина внутрішньої бісектриси} \ \ \alpha = \frac{2 \sqrt{bcs(s-a)}}{b+c} = \sqrt{bc[1- \frac{a^{2}}{(b+c)^{2}}]}](https://upload.wikimedia.org/math/c/a/a/caab63ffb53415bd8261363eac1cd515.png)






Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.