Матеріал з Вікіпедії — вільної енциклопедії.
Ізометрія, або рух, або (рідше) накладення — бієкція (перетворення), яка зберігає відстань між відповідними точками, тобто якщо 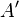 і
і  — образи точок
— образи точок  і
і  , то
, то  . Термін «ізометрія» поширеніший в метричній геометрії, зокрема, в рімановій геометрії. У загальному випадку метричного простору (наприклад, для неплоских ріманових многовидів) руху можуть існувати далеко не завжди.
. Термін «ізометрія» поширеніший в метричній геометрії, зокрема, в рімановій геометрії. У загальному випадку метричного простору (наприклад, для неплоских ріманових многовидів) руху можуть існувати далеко не завжди.
Термін «рух» поширеніший в евклідовій геометрії і суміжних областях.
У евклідовому (або псевдоевклідовому) просторі ізометрія автоматично зберігає також кути, тобто, зберігаються всі скалярні добутки.
У цій статті нижче мається на увазі евклідів простір.
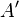 і
і  — образи точок
— образи точок  і
і  , то
, то  . Термін «ізометрія» поширеніший в метричній геометрії, зокрема, в рімановій геометрії. У загальному випадку метричного простору (наприклад, для неплоских ріманових многовидів) руху можуть існувати далеко не завжди.
. Термін «ізометрія» поширеніший в метричній геометрії, зокрема, в рімановій геометрії. У загальному випадку метричного простору (наприклад, для неплоских ріманових многовидів) руху можуть існувати далеко не завжди.Термін «рух» поширеніший в евклідовій геометрії і суміжних областях.
У евклідовому (або псевдоевклідовому) просторі ізометрія автоматично зберігає також кути, тобто, зберігаються всі скалярні добутки.
У цій статті нижче мається на увазі евклідів простір.
Зміст
Види ізометрії
На площині
- Осьова симетрія (відбиття);
- Паралельний перенос;
- Обертання;
- Ковзна симетрія — композиція переносу на вектор, що паралельний до прямої, і симетрії цієї прямої.
У тривимірному просторі
- Дзеркальна симетрія (відбиття) щодо площини;
- Паралельний перенос;
- Поворот;
- Ковзна симетрія — композиція перенесення на вектор, що паралельний до площини, і симетрії цієї площини;
- Дзеркальне обертання — композиція повороту навколо деякої прямої і відбиття відносно площини, що перпендикулярна осі повороту;
- Гвинтове накладання — композиція повороту відносно деякої прямої і перенесення на вектор, що паралельний цій прямій.
У n-вимірному просторі
У -мірному просторі рухи зводяться до всіх ортогональним перетворень, паралельних переносів і композицій того й іншого.
-мірному просторі рухи зводяться до всіх ортогональним перетворень, паралельних переносів і композицій того й іншого.У свою чергу ортогональні перетворення можуть бути представлені як композиції (власних) обертань і дзеркальних відбиттів.
Загальні властивості ізометрії
- Композиція ізометрій також є ізометрією.
- Ізометрії щодо композиції утворюють групу.
- Ізометрия — афінне перетворення.
- Ізометрия переводить відрізок у відрізок.
Рухи як композиції симетрій
Композиція двох відбиттів щодо незбіжних паралельних осей дає паралельний перенос.
Композиція двох відбиттів щодо непаралельних осей дає поворот.
 -мірному евклідовому просторі можна представити у вигляді композиції не більше ніж
-мірному евклідовому просторі можна представити у вигляді композиції не більше ніж  відбиттів.
відбиттів.Так, паралельний перенос і поворот — композиції двох відбиттів, ковзне відбиття і дзеркальний поворот — трьох, гвинтове накладення — чотирьох.


Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.