Матеріал з Вікіпедії — вільної енциклопедії.
Загальні відомості
Квадратні рівняння є різновидом рівнянь другого степеня з однією змінною. Числа — його коефіцієнти, при чому
— його коефіцієнти, при чому  також називається першим коефіцієнтом,
також називається першим коефіцієнтом,  — другим,
— другим,  — вільним членом. Будь-яке квадратне рівняння має
— вільним членом. Будь-яке квадратне рівняння має- або два різних дійсних корені,
- або два однакові дійсних корені (тобто, по суті, один),
- або взагалі не має дійсних коренів, а має два комплексні корені.
 та
та  або, якщо йдеться про обидва корені одночасно, то
або, якщо йдеться про обидва корені одночасно, то  В деякій літературі зустрічається ще й таке позначення:
В деякій літературі зустрічається ще й таке позначення:  і
і  .)
.)Неповні квадратні рівняння
Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо , то
, то  перетворюється у лінійне рівняння
перетворюється у лінійне рівняння 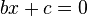 . Якщо хоч один коефіцієнт
. Якщо хоч один коефіцієнт  або
або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:
дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів: ;
;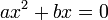 ;
;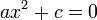 .
.
Розв'язування неповних квадратних рівнянь
- Рівняння виду
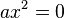 рівносильне рівнянню
рівносильне рівнянню  і тому завжди має тільки один корінь
і тому завжди має тільки один корінь  .
. - Рівняння виду
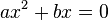 розв'язується винесенням за дужки
розв'язується винесенням за дужки  :
:  . Таке рівняння має два корені:
. Таке рівняння має два корені: 
- Квадратне рівняння виду
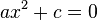 рівносильне рівнянню
рівносильне рівнянню  . Якщо
. Якщо  , воно має два дійсних розв'язки, якщо
, воно має два дійсних розв'язки, якщо 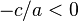 — жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то
— жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то 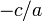 додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число
додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число 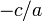 від'ємне і
від'ємне і 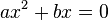 не має дійсних коренів.
не має дійсних коренів.
Повне квадратне рівняння
Повним називається таке квадратне рівняння, у якому жодний з коефіцієнтів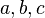 не дорівнює нулю.
не дорівнює нулю.Дискримінант
 .
.Помноживши обидві частини рівняння
 на
на  , дістанемо:
, дістанемо: ,
,
 .
.
Розв'язування повних квадратних рівнянь
Якщо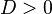 , то квадратне рівняння рівносильне рівнянню
, то квадратне рівняння рівносильне рівнянню  , звідки
, звідки . Коротко ці корені записують так:
. Коротко ці корені записують так: , де
, де 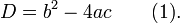
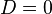 , то
, то  , звідки
, звідки 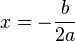 — єдиний корінь (правильніше - два однакові корені)
— єдиний корінь (правильніше - два однакові корені)У випадку, якщо дискримінант менший за нуль, то дане рівняння не має дійсних коренів. Але при цьому є можливість знайти два комплексних корені за формулою (1) або, скориставшись наступною формулою, щоб не добувати корінь з від'ємного числа:
 де :
де :
Зведені квадратні рівняння
Зведеними називаються такі квадратні рівняння, у яких перший коефіцієнт дорівнює одиниці —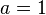 . Будь-яке квадратне рівняння можна перетворити у зведене, іншими словами, звести його. Для цього треба обидві частини рівняння поділити на
. Будь-яке квадратне рівняння можна перетворити у зведене, іншими словами, звести його. Для цього треба обидві частини рівняння поділити на  :
:Теорема Вієта
Якщо зведене квадратне рівняння має два корені, то їх сума дорівнює другому коефіцієнтові рівняння, взятому з протилежним знаком, а добуток — вільному члену. Для прикладу візьмемо зведене рівняння і позначимо
і позначимо  через
через  а
а 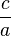 через
через  Тоді воно матиме такий вигляд:
Тоді воно матиме такий вигляд:Доведення
Якщо рівняння має корені
має корені  і
і  то їх можна знаходити за формулами:
то їх можна знаходити за формулами: і
і 
Теорема обернена до теореми Вієта
Якщо сума і добуток чисел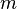 і
і 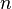 дорівнюють відповідно
дорівнюють відповідно  і
і  , то
, то 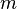 і
і 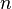 — корені рівняння
— корені рівняння  .
.Використання теореми Вієта та оберненої до неї
Використовуючи теорему Вієта можна перевіряти правильність розв'язання квадратних рівнянь. А користуючись оберненою теоремою, можна навіть усно розв'язувати більшість зведених рівнянь. Для прикладу розв'яжемо таке рівняння:Інші методи розв'язування
Для знаходження коренів існують формули, які можуть стати в нагоді у деяких часткових випадках. Так, наприклад, формулуТакож поширеною є формула
 .
Тобто у випадку відсутності вільного члена з допомогою неї не вдасться
добути другий корінь (перший дорівнюватиме нулю). Цю проблему можна
вирішити використовуючи змішаний вигляд вищезазначеної формули:
.
Тобто у випадку відсутності вільного члена з допомогою неї не вдасться
добути другий корінь (перший дорівнюватиме нулю). Цю проблему можна
вирішити використовуючи змішаний вигляд вищезазначеної формули: — sign-функція. Цей спосіб розв'язування рівнянь дещо простіший за звичайний метод і позбавлений недоліку формули (2).
— sign-функція. Цей спосіб розв'язування рівнянь дещо простіший за звичайний метод і позбавлений недоліку формули (2).Аналітична геометрія
Графік функції y = x2 − x − 2 перетинає вісь абсцис у точках з координатами, що дорівнюють кореням рівняння x2 − x − 2 = 0
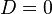 , графік дотикається до неї в одній точці; якщо ж дискримінант менший за нуль, графік не перетинає вісь Ox взагалі.
, графік дотикається до неї в одній точці; якщо ж дискримінант менший за нуль, графік не перетинає вісь Ox взагалі.Факторизація
Ліва частина квадратного рівняння, яка також називається квадратним тричленом, може бути розкладена на множники за такою формулою: , де
, де  — корені цього рівняння.
— корені цього рівняння.Рівняння, що зводяться до квадратних
До квадратних можна звести біквадратне, а також будь-яке рівняння виду , зробивши заміну
, зробивши заміну  . Для прикладу розв'яжемо наступне рівняння:
. Для прикладу розв'яжемо наступне рівняння: :
: легко знайти корені початкового рівняння:
легко знайти корені початкового рівняння:Історія
розв'язування рівнянь другої степені, в тому числі й квадратних, у стародавні часи була викликана потребою вирішувати проблеми пов'язані з поділом землі, знаходженням її площі, земельними роботами військового характеру, а також із розвитком таких наук, як математика й астрономія. Квадратні рівняння вміли вирішувати вавилоняни близько 2000 років до н.е. Серед клинописних текстів були знайдені приклади розв'язання неповних, а також часткових випадків повних квадратних рівнянь. Відомо, що їхні методи розв'язання майже збігаються із сучасними, проте невідомо, яким чином вавилоняни дійшли до цих методів: майже на всіх знайдених до того часу клинописних текстах збереглися лиш вказівки до знаходження коренів рівнянь, але не вказано, як вони були виведені. Однак, не зважаючи на розвинутість математики у ті часи, в цих текстах немає ані найменшої згадки про від'ємні числа і про загальні методи розв'язання рівнянь.В стародавній Греції квадратні рівняння розв'язувалися за допомогою геометричних побудов. Методи, які не пов'язувалися з геометрією, вперше наводить Діофант Александрійський у III ст. У своїх книгах «Арифметика» він наводить приклади розв'язування неповних квадратних рівнянь. Його книги з описом способів розв'язання повних квадратних рівнянь до нашого часу не збереглися.
Правило знаходження коренів рівняння, зведеного до вигляду
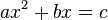 уперше дав індійський вчений Брахмагупта.
уперше дав індійський вчений Брахмагупта.Аль-Хорезмі описав алгоритм для знаходження коренів всіх шести підвидів квадратного рівняння.
Загальне правило розв'язання квадратних рівнянь було сформоване німецьким математиком М. Штифелем (1487 — 1567). Виводом формули загального розв'язку квадратних рівнянь займався Франсуа Вієт. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жирара (1595 — 1632), а також Декарта і Ньютона спосіб розв'язання квадратних рівнянь набув сучасного вигляду.
 де
де  .
.























![x_1 = \sqrt[3]{t_1} = \sqrt[3]{2},](https://upload.wikimedia.org/math/a/0/3/a0320a18715acaeba6fcaac4e91d2555.png)
![x_2 = \sqrt[3]{t_2} = \sqrt[3]{5}.](https://upload.wikimedia.org/math/c/5/9/c593122c1c2181969ae7ddd97a36750e.png)
Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.