Матеріал з Вікіпедії — вільної енциклопедії.
Теоре́ма Віє́та — формули, названі на честь Франсуа Вієта, що виражають коефіцієнти многочлена через його корені.
Ці формули зручно використовувати для перевірки правильності знаходження коренів та для задання многочлена з визначеними властивостями.
Ці формули зручно використовувати для перевірки правильності знаходження коренів та для задання многочлена з визначеними властивостями.
Формули
Якщо — корені многочлена
— корені многочлена  (кожен корінь присутній відповідно до його кратності),
(кожен корінь присутній відповідно до його кратності),то коефіцієнти
 виражаються в вигляді симетричних многочленів від коренів, а саме:
виражаються в вигляді симетричних многочленів від коренів, а саме: дорівнює сумі всіх можливих
дорівнює сумі всіх можливих 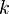 -добутків із коренів.
-добутків із коренів.Якщо старший коефіцієнт многочлена
 , то для застосування формули Вієта необхідно розділити всі коефіцієнти на
, то для застосування формули Вієта необхідно розділити всі коефіцієнти на 
Із останньої формули Вієта випливає, що якщо корені многочлена є цілими, то вони є дільниками його вільного члена, який також є цілим.
Доведення
Доведення використовує рівністьПісля відкриття дужок, коефіцієнти при однакових степенях x повинні бути однаковими в обох частинах, з чого слідують формули Вієта.
Приклади
- Якщо
 корені квадратного рівняння
корені квадратного рівняння  то
то
- В частковому випадку при
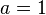 (квадратне рівняння
(квадратне рівняння  ), то
), то




Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.