Матеріал з Вікіпедії — вільної енциклопедії.
Кубі́чне рівня́ння — алгебраїчне рівняння виду
 після чого провівши заміну змінної
після чого провівши заміну змінної 
При цьому коефіцієнти будуть рівні:
 , де
, де  .
.
 після чого провівши заміну змінної
після чого провівши заміну змінної 
При цьому коефіцієнти будуть рівні:
Метод Кардано
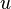 та
та 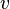 , такі що
, такі що отримаємо та розв'яжемо квадратне рівняння відносно
отримаємо та розв'яжемо квадратне рівняння відносно  наступним чином:
наступним чином: один з них є
один з них є та:
та: то рівняння має один дійсний корінь і два комплексні.
то рівняння має один дійсний корінь і два комплексні. то всі три корені рівняння є різними дійсними числами.
то всі три корені рівняння є різними дійсними числами. то всі корені рівняння є дійсними числами, при чому принаймні два з них є однаковими.
то всі корені рівняння є дійсними числами, при чому принаймні два з них є однаковими.
Приклад
Розв'яжемо рівняння з очевидними коренями -1, 0, +1:
з очевидними коренями -1, 0, +1:





![z=\sqrt[3]{-\frac{q}{2}+ \sqrt{D}} +\sqrt[3]{-\frac{q}{2}- \sqrt{D}}.](https://upload.wikimedia.org/math/a/4/4/a443f1dd3c48d7bc8d8f33523932470f.png)

Немає коментарів:
Дописати коментар
Примітка: лише член цього блогу може опублікувати коментар.